Оценка проектного риска при создании сложных технических систем Опубликовано в
журнале
Известия вузов. Сер. "Приборостроение", И.В. Минаев, С.В. Рубцов
Проектирование сложных технических систем (СТС) часто приводит к ситуации, когда оценка адекватности проектных решений требованиям, формируемым в техническом и частных технических заданиях (ТЗ и ЧТЗ) на разработку СТС и ее элементов, становится трудно разрешимой задачей [1]. Сложившееся положение обусловлено наличием следующих факторов неопределенности, снижающих обоснованность принимаемых решений:
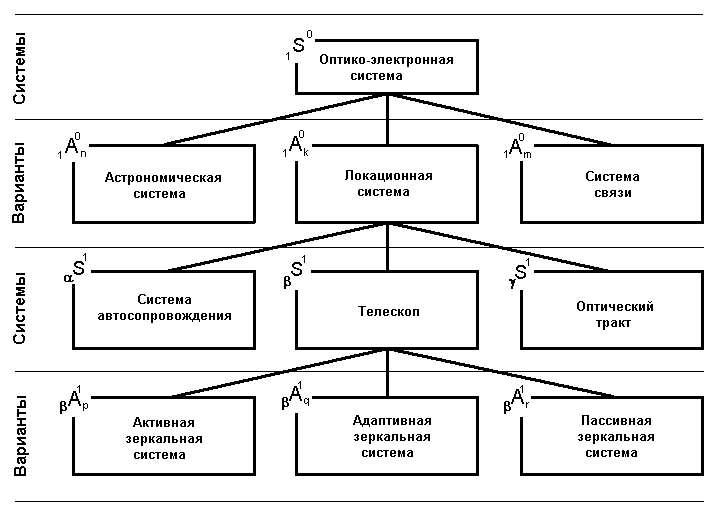
Следствием описанной трудности синтеза рационального облика СТС явилось формирование в настоящее время концепции автоматизированных систем поискового конструирования (АСПК) второго поколения [3] с элементами искусственного интеллекта, для которых краеугольной задачей является представление эвристических соображений проектировщика в виде формальных правил и операций. К этому классу задач может быть отнесена задача принятия проектных решений для СТС в соответствии с эвристической процедурой, реализующей принцип последовательно-параллельного формирования "сверху-вниз" ЧТЗ на разработку ее подсистем. Характерным примером такой проектной задачи является задача выбора из множества альтернативных вариантов построения оптико-электронных систем (ОЭС) [1]. На рис.1 представлена возможная декомпозиция ОЭС как объекта АСПК.
Рис. 1. Инфологическая модель оптико-электронной системы Одним из проблемных вопросов при реализации проектной процедуры является учет возрастающего влияния перечисленных факторов неопределенности при последовательной детализации описания облика СТС различного уровня иерархии. Наличие факторов неопределенности обусловливает присутствие риска невыполнения требований ТЗ на разработку СТС и необходимость поиска способов его оценки. В данной статье, являющейся дальнейшим развитием общего подхода к оценке адекватности требованиям ТЗ принимаемых проектных решений [1, 4, 5], предлагается универсальный для задач анализа и синтеза СТС метод оценки проектного риска как степени достижимости иерархической системы взаимосвязанных целей проектирования СТС. В общем случае ТЗ, формируемое проектными организациями, представляет собой набор глобальных целей, задающих основные направления исследований в процессе выработки проектных решений. Часто эти цели представляют собой утверждения общего характера относительно качества и особенностей выполнения отдельных функций СТС или неточные формулировки ограничений, которые в сумме составляют пожелания, требования, потребности и т.д. Тем самым создается проблемная ситуация, в которой проектировщик сталкивается с необходимостью восприятия и представления вызывающих сомнений неточных и нечетких понятий. Для представления ТЗ, ЧТЗ и технического описания вариантов какого-либо технического решения в формализованном виде введем обозначение цели проектирования и свойства технического решения: <Цель>=<Понятие & "Интенсивность" проявления>, <Свойство>=<Понятие & "Интенсивность" проявления >, где категория <понятие> определяет смысловое (понятийное) описание свойства СТС, а <"интенсивность" проявления>, являющаяся лингвистической переменной [6], характеризует требуемый качественный уровень этого свойства с точки зрения свойства более высокого уровня в случае описания цели проектирования, а при описании свойства является результатом оценки качества рассматриваемого варианта относительно других вариантов построения элементов СТС как независимого объекта. Например, если 01G00=Us01g0s0 - формализованное представление ТЗ, интерпретируемое на языке теории нечетких множеств [6, 7, 9] в качестве групповой цели, являющейся объединением частных целей 01g0s0 как нечетких множеств, то в соответствии с формализованным определением нечеткой цели 01 g0s0 = <1xs0 & 01L0s0>,где 01L0s0 - "интенсивность" проявления свойства СТС, определяемого понятием 1xs0, соответствующая потребности заказывающей организации. Введем следующую систему обозначений: d Amn - m-й вариант решения dSn n-го уровня иерархии;d Mnpm - "интенсивность" проявления свойства варианта dAmn, определяемого понятием dxpn;d vnpm(u) - функция принадлежности [7], описывающая "интенсивность" dMnpm как нечеткое множество, с областью определения, задаваемой числовой шкалой U= {u}с мощностью разбиения П0(U);d Gn = Up dgpn - групповое свойство варианта dAmn решения dSn;d gpn = <dxpn & dMnpm> - р-е свойство варианта dAmn;cd Gqn = Upcdgnpq - групповая цель разработки решения dSn, определяемая групповым свойством cG n-1 (n-1)-го уровня, где c -номер рассматриваемого на (n-1)-м уровне решения cS n-1, включающего в себя решение dSn;cdg npq = < dxpn & cdL npq> - частная цель проектирования для решения dSn; cdL npq - требуемая "интенсивность" проявления свойства dgpn для достижения заданного качественного уровня свойства cgq n-1; cdµ npq(u) - функция принадлежности, описывающая степень соответствия cdLnpq как нечеткого множества, с областью определения U={u}; dX n = Up dxpn - система понятий, составляющая основу смыслового описания свойств { dgp n }и целей { cdg npq }; cdHnpq - степень смысловой близости понятий dxpn и cxq n-1, определяемая через операцию несимметрической разности в терминах теории нечетких множеств [7]; cdfpn - функция принадлежности, задающая нечеткое бинарное отношение важности на множестве целей { cdg npq } : cdGqn * cdGqn -> [0, 1] с учетом групповой цели cG n-1. Меру достижимости частной цели cdg npq при выборе варианта dAmn с точки зрения достижимости свойства cgq n-1 определим показателем cdmEnpq, выражающим смысловую близость параметров cdL npq и dM npm. В интерпретации теории нечетких множеств [8] cdm Enpq = [1-SUMu |dvnpm(u) - cdµ npq(u)| ] / (П0(u) + SUMu min[dvnpm(u),cdµ npq(u)]). Достижимость группового свойства cGn-1 = Uq cgq n-1 при выборе варианта dAmn может быть оценена с использованием алгоритма F, предложенного в [9] для вычисления функции принадлежности I объекта произвольной природы недоминируемому множеству решений: F [cdmR n-1kr , bcT n-1q] -> t(cG n-1) = cdmB n,n-1; cdm R n-1kr = (cdmB n,n-1 - cdmB n,n-1 + 1) / 2,где cdmB n,n-1 - мера достижимости свойства cgq n-1 при выборе варианта dAmn, которая при минимальной интерпретации [7] может быть определена следующим образом: cdm B n,n-1 = argmax { cdmB n,n-1 (dAmn)}, по dAmn ,где dA*n - выбранный вариант решения dS n. Пусть cdB n,n-1 = cd*B n,n-1. Тогда оценка достижимости группового свойства cG n-1 решения cS nn-1 по окончании выбора на множестве всех решений n-го уровня, входящих в решение cS nn-1, определяется посредством операции пресечения нечетких множеств: b B n,n-1 = mind (cdB n,n-1). Аналогично можно оценить степень достижимости b B n,n-2 групповой цели сформулированного в описании решения b S n,n-2 (n-2)-го уровня при завершении выбора решения (n-1)-го и n-го уровней иерархии, входящих в решение b S n,n-2. b B n,n-2 = min (cB n,n-1, bB n-1,n-2). Таким образом, представленная выше система соотношений определяет рекуррентный процесс выбора вариантов технических решений на различных иерархических уровнях декомпозиции СТС и оценки степени достижимости "интенсивности" проявления свойств, заданных в ЧТЗ различного уровня и ТЗ на разработку СТС. На рис.2 данный процесс представлен в виде сетевого графика, определяющего порядок вычисления основных показателей качества принимаемых проектных решений.Из последней формулы следует неравенство: b B n,n-2 <= bB n-1,n-2, выражающее тот факт, что существует рациональная глубина проводимого при проектировании СТС анализа решений (как по уровням иерархии, так и по мощности множества вариантов), обусловленная возрастанием влияния факторов неопределенности , при которой степень достижимости целей будет ниже заданной, или, другими словами, при которой требования ТЗ на разработку СТС будут удовлетворяться с заданной степенью риска. Таким образом, описанный метод оценки степени достижимости целей проектирования СТС может быть использован в АСПК как для решения задачи выбора на множестве вариантов построения СТС, формирования допустимых вариантов для заданной степени достижимости целей, оценки степени соответствия решения требованиям ЧТЗ различных уровней и ТЗ, так и анализа интерпретируемого в смысле степени достижимости целей уровня риска невыполнения ТЗ на разработку СТС. ЛИТЕРАТУРА1. Минаев И.В., Рубцов С.В. Устойчивость принципов оптимальности процесса гибкого формирования облика сложной системы//Изв.вузов СССР. Приборостроение. - 1989. - Т. 32, №3.- С. 69-73. 2. Дружинин В.В., Конторов Д.С. Системотехника.- М.: Радио и связь, 1985. 3. Камаев В.А., Никитин С.В., Залевская Ф.Я. Поисковое конструирование//Итоги науки и техники. Техн. Кибернентика / ВИНИТИ. - 1986.- №19. - С. 142-189. 4. Минаев И.В., Рубцов С.В. Оценка эффективности модеризации оптико-электронных систем//Изв.вузов СССР. Приборостроение.-1987.-Т.30, №11.-С.67-71. 5. Минаев И.В., Мордовин А.А., Шереметьев А.Г. Лазерные информационные системы космических аппаратов.-М.: Машиностроеие.1981 6. Заде Л.А. Понятие лигвистической переменной и ее применение к принятию приближенных решений.- М.: Мир, 1976. 7. Кофман А. Введение в теорию нечетких множеств. - М.:Радио и связь, 1982. 8. Driankov D. An outline of a fuzzy sets approach to decision making with interdependent goals// Fuzzy Sets and Systems.- 1987.-Vol.21.-P.275-288. 9. Орловский А. Проблемы принятия решений при нечеткой исходной информации. - Москва: Наука, 1982.- 206.
|
||||||